[월가 아재] [월가아재 시즌3 - 36편] 과도한 재정지출은 인플레로 이어지는가? 매크로 데이터의 위험성

LINK : https://www.valley.town/join

■ Preview

재정지출은 인플레와 주가 하락으로 이어지는가?

● 대선 전 6개월 vs 대선 후 6개월 데이터

● 귀납적 추론과 연역적 추론

● 데이터의 한계와 통계적 유의미성

■ 대선 이후

가장 중요한 포인트 : 경기 침체 vs 인플레이션 재점화 

지난 시간 : 1960~70년대 vs 2020년대, 스태그플레이션의 역사

● 솔직히 70년대와 같이 두 자릿 수 인플레가 지속되는 시대가 펼쳐질 가능성에는 회의적

● 현재 연준은 훨씬 더 정치적으로 독립적이고, 많은 경험과 도구를 보유

● 그러나 과거에 비해 금리 상승에 대한 면역이 매우 낮아진 상태 

→ 과거에 비해 전세계적인 부채 수준이 높아졌고, 금리 상승에 대한 면역이 체질적으로 매우 약해진 상태

● 절대적으로 높은 수준의 인플레가 아니더라도, 2%보다 조금 높은 수준의 인플레가 지속되고,

● 그것이 장기채 공급 우려와 맞물리면 상당한 리스크 요인

→ 금융 위기 이후 만연한 좀비기업, 중소형 은행, 미국의 State Pension 시스템 등

특히 경기 침체가 찾아왔을 때 2~3%대에서 Sticky한 모습을 보일 경우

● 연준이 완화적 통화정책을 펴는데 큰 걸림돌 

● 금융위기 이후 16년간 이어졌던 Fed Put에 대한 신뢰를 무너뜨리면서 자산에 시장에 타격을 입힐 수 있음

그러나, 거대담론으로 눈앞의 의사결정을 하지 말자

지난 시간 마지막: 대선 직전 6개월 vs 대선 직후 6개월 주가 수익률 비교

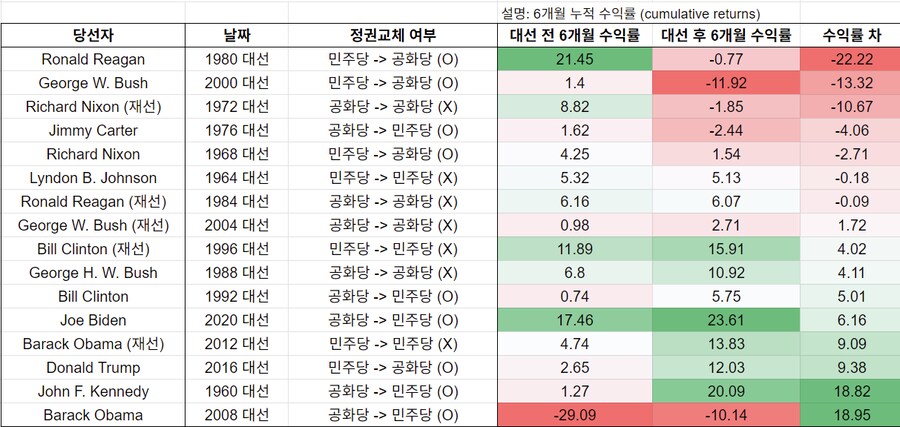60년간 16번의 대선: 대선 전 6개월은 4.15% vs 대선 후 6개월은 5.65% → 대선 전후 매수?

→ 통계의 남용

■ 귀납적 추론

귀납적 추론

● 1번 백조를 봤더니 하얗다, 2번 백조를 봤더니 하얗다... 모든 백조는 하얗다

● 과거 사례를 통한 일반화 → 미래를 추정

● AI와 머신러닝의 근간 = 과거 데이터를 통한 패턴 인식

데이터에 기반한 귀납적 추론의 요건

1. 데이터의 개수가 충분

2. 각 데이터가 비슷한 환경에서 수집되어야 함

■ 5분 기초 통계

5분 기초 통계 Ⅰ

외계인이 사는 새로운 별 발견, 외계인의 평균 키를 추정해 보자

● 외계인 1명의 키 132cm → 외계인 인구의 평균 키는 132cm다?

● 외계인 10명의 평균 키 147cm → 외계인 인구의 평균 키는 147cm다?

● 외계인 100명? 1000명?

● 샘플 수가 많아질수록 그 샘플의 평균 키 = 전 인구의 평균 키에 대한 확신 ↑

→ 법칙 1 : 데이터의 개수가 많아질수록, 그 평균에 대한 신뢰도는 높아진다

※ 큰 수의 법칙 : 표본의 크기가 커질수록 표본 평균이 모평균에 가까워진다

5분 기초 통계 Ⅱ

외계종 A, B가 존재

● A 외계인 5명 : 143cm, 142cm, 145cm, 142cm, 143cm → 평균 143cm

● B 외계인 5명 : 45cm, 321cm, 140cm, 50cm, 159cm → 평균 143cm

● 어떤 추정이 더 믿을만한가? B외계인 샘플은 너무 들쭉날쭉

→ 법칙 2 : 관측된 데이터가 들쭉날쭉할수록, 그 평균에 대한 확신은 낮아진다

※ 데이터의 변동성(또는 분산, 표준편차)에 따른 신뢰성의 차이

어떤 샘플을 관측하고 그 샘플의 평균을 냈을 때,

그 평균값(표본 평균)이 전체 인구의 실제 평균값(모평균)과 비슷할 가능성은

1) 데이터가 많을수록, 2) 수치가 덜 들쭉날쭉할수록 높아진다

5분 기초 통계 Ⅲ

데이터가 많고, 수치가 덜 들쭉날쭉할수록, 신뢰구간/오차범위가 좁아진다 = 더 정확해진다

● 외계인 50명 평균 키 140cm, 표준편차(들쭉날쭉함) 18cm = 95% 신뢰구간은 약 135~145cm

● 외계인 500명 평균 키 140cm, 표준편차(들쭉날쭉함) 18cm = 95% 신뢰구간은 약 138.4~141.6cm 

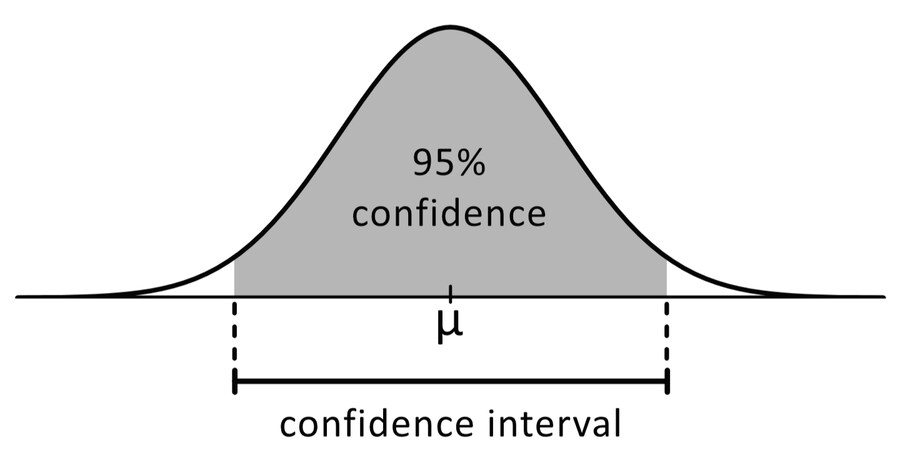
95% 신뢰구간이 135~145cm라 함은 (엄밀하지는 않지만)

실제 외계인 인구의 평균 키가 135~145cm 안에 있을 가능성이 95% 정도라는 뜻

나머지 5% 확률은 내가 우연히 농구선수인 외계인들만 50명 관찰하게 된 케이스일 가능성을 의미

예) 트럼프, 해리스의 지지율이 오차범위 내에서 누군가가 더 높다

= 평균은 한 쪽이 더 높긴 하지만, 신뢰구간이 서로 겹친다

= 그래서 샘플을 바탕으로 확실히 통계적으로 유의미한 결론을 내를 수 없다

■ 대선 수익률의 평균과 표준편차

우리가 알고 싶은 것은 "대선 전 6개월 기대수익률"의 어떠한 진리값 x 

→ 외계인의 예시에 비유하면 전체 인구의 평균 키 (모평균)

16번의 대선 샘플을 관찰한 결과 평균 수익률이 4.15%, 표준편차가 10.71% 나왔다면

→ 실제 X는 95% 확률로 -1.56% ~ 9.86% 어딘가에 있다는 쓸모없는 결론

대선 전 6개월에 투자할 경우 기대수익률은 -1.56% ~ 9.86% 범위 중 어딘가이다

대선 후 6개월에 투자할 경우 기대수익률은 0.29% ~ 11.02% 범위 중 어딘가이다

→ 이 샘플로는 대선 전 6개월 수익률보다 대선 후 6개월 수익률이 더 월등하다는 통계적 근거가 희박하다는 의미

■ 시계열의 비정상성 (Nonstationarity)

한국인의 평균키를 추정하고자 한다

● 1960년대에서 5명, 1970년대에서 5명... 2020년대에서 5명을 뽑아 평균을 내면?

● 시대별로 영양을 비롯한 환경들이 다름

매크로 데이터의 문제점

● 1960년대부터 2020년대까지 60년에 걸쳐 듬성듬성 뽑은 데이터

● 공통점이라고는 '대선' 밖에 없고, 각기 다른 환경의 데이터를 평균낸 값

● 마치 60년대 사람들과 2020년대 사람들을 섞어 놓고 평균을 재는 것

■ 매크로에서 귀납적 추론의 어려움

매크로 지표들은 보통 분기/연 단위 → 10년치 데이터를 보아도 데이터 개수가 부족

● 이를 극복하기 위해 점점 더 과거의 데이터를 사용하면 할수록, 매크로 데이터가 서로 다른 샘플이 뒤섞이는 문제 발생

이런 오용을 전문가들이 모를까?

● 많은 경우, 그게 할 수 있는 최선이라서

● 엄밀하지 않고 오용일 수 있더라도, 그러한 데이터와 통계를 사용

● 월가아재 유튜브에서도 자주 오용 → 예시 : 섹터 로테이션

→ 과거 경기 사이클 지점에서 섹터 수익률을 보여줌 

→ 10개에서 많아야 15~20개 정도의 데이터 포인트에서 평균값/중앙값을 뽑아 쓰기 때문에 오차범위가 굉장히 큼

● 그럼에도 불구하고, 데이터 측면에서 귀납적으로 우리가 할 수 있는 최선이 그것...

■ 매크로에서 데이터를 논할 때 명심할 점

1. 통계적으로 유의미성이 부족한 데이터를 사용한다면, 적어도 그 맹점을 인지하고 사용할 것

→ 예시 : 해리스 vs 트럼프 지지율을 논할 때 "오차 범위 내에서" 앞선다는 수식어를 붙이는 것

2. 귀납적 평균은 참조만 할 뿐, 결국은 그 인과 관계에 집중해서 연역적 추론을 하기 위해 최선을 다할 것

연역적 추론

● 재정지출이 과도 → 인플레이션 발생 → 연준이 금리 인상 → 듀레이션이 높은 미래산업이 하락

● 경제학적 명제들을 논리적으로 이어서 결론을 도출하는 방식

■ 부족한 데이터로 어떻게 더 나아갈 수 있을까?

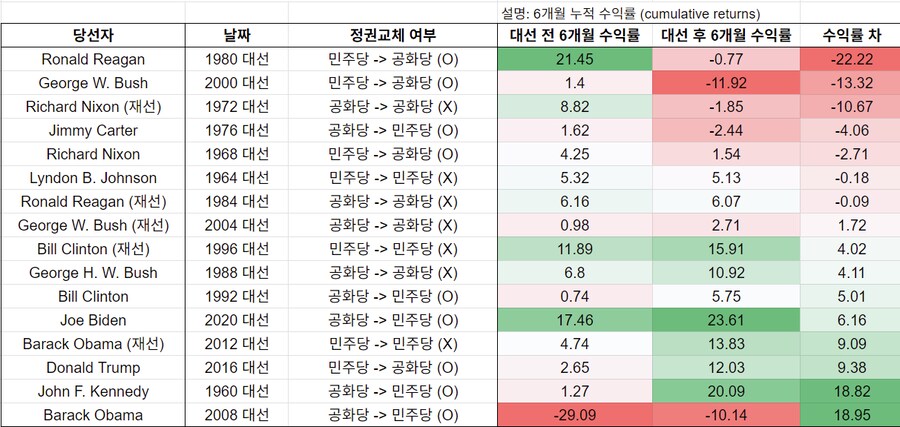
우리는 과거 사이클이나 패턴을 참고하기는 하되,

나이브한 결론보다는 반드시 왜 그랬는지, 논리에 기반해 풀어낼 필요

→ 과거 사례들은 해당 케이스 속 경제학적 명제를 공부하기 위해 활용

■ 재정지출에 뒤따르는 인플레

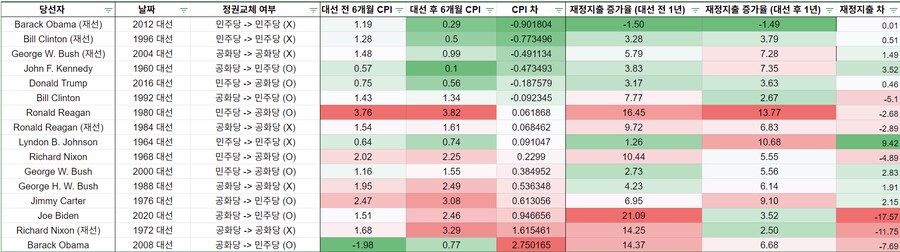
우리가 걱정하는 부분 : 재정지출에 뒤따르는 인플레이션

● 과도한 재정지출로부터 6~9개월 후에 시차를 두고 인플레이션이 발생한다

● 인플레이션은 주가에 좋지 않다

CPI를 추가하면, 16번의 대선 중

● 6번은 대선 후 인플레 하락 → 6번 주가 상승 (100%) 

● 10번은 대선 후 인플레 상승 → 7번 주가 하락 (70%)

기존의 나이브한 결론 : "대선 전보다 대선 후가 수익률이 좋다" 에서 

→ 대선 후 CPI가 더 낮아지면, 주가는 좋고

→ 대선 후 CPI가 더 높아지면, 주가는 나쁘다

이처럼 조금 더 논리적으로 정교한 명제를 도출 (교락 변수인 CPI를 추가)

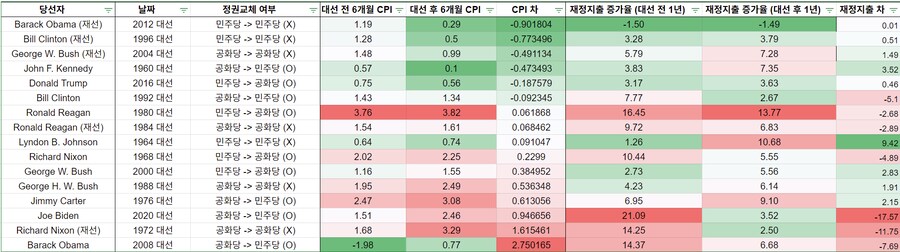
CPI말고, 재정지출 증가율도 같이 들여다 보자

● <대선 전후 CPI 차이> 와 

● <대선 전 1년 재정지출 증가율의 추이>의 상관관계는 0.62

● 대선이 있는 해에 정부가 재정지출을 많이 한 경우,

● 대선 이후 CPI가 더 높아지는 결과로 이어지는 경향이 있다

대선이 있는 해 재정지출 → 대선 이후 CPI 상승 → 주가 하락

이 논리가 적어도 이 데이터 상으로는 부합

<대선 전후 CPI 차이>와 <대선 후 재정지출 차>의 상관관계는 -0.54

● 대선 이후 CPI가 높아지면, 정부는 재정지출을 줄이는 경향이 있다 

● 2024년의 재정지출 → 대선 후 인플레 재점화 → 재정지출 줄일 가능성 + 주가 하락

→ 2024년에 옐런이 재정지출을 많이 해서, 대선 이후 6개월 동안 CPI가 높게 나오면, 2025년에는 재정지출을 줄이고 허리띠를 졸라맬 가능성이 높다

이렇게 통계적 유의미성이 낮은 데이터라도,

우리가 알고 있는 경제학적 명제들을 논리적으로 연결해 연역적 추론을 할 때,

크로스 체크하는 용도로 이러한 귀납적 추론을 활용할 수 있음

■ 하드 사이언스 vs 소프트 사이언스

금융AI 분야 : 많은 데이터 → 머신러닝 및 다양한 통계적 기법, 귀납적 추론

심리학 분야 : 인간을 대상으로 해서 적은 데이터 → 정성적 리서치, Case Study 등 

→ 매크로는 전자보다 후자에 더 가까운 영역

→ 기업분석, DCF 분야도 마찬가지 

→ 개별 기업이 속한 산업 환경, 경영진의 역량 등 개별 특수성이 많은 데이터를 봐야하기 때문

→ 그래서 기술적 분석/데이 트레이딩은 퀀트들이 장악하고 있지만,

매크로 분석/가치투자는 휴먼 애널리스트와 펀드 매니저들이 꽤 많은 편 (미국 헤지펀드 중에서 펀더멘털 기반 투자를 하는 펀드)

■ 케이스 스터디의 중요성

방금 예시에서도, CPI에 영향을 미치는 변수들은 재정지출 외에도 유가와 같은 다양한 외생적 변수 존재

→ 각 대선에 대한 케이스 스터디가 필요

■ 현 시황

결국 10, 11, 12월뿐만 아니라 내년 상반기까지

● 최근 재무부 QRA 국채 발행 계획을 들여다본 것처럼

● 국채 발행 추이, 재정지출 추이, TGA 잔고, CPI 등을 주시하면서

● 다음 QRA + 부채한도 협상 모니터링

● 경기 침체 조짐에 대해서도 주시

결국 경기침체 vs 인플레 어떤 압력이 강할지, 예측하는 것은 매우 힘든 일

● 그러나 적어도 오늘의 사고과정을 통해

● 무엇을 주시해야할지, 왜 주시해야 하는지, 아는 사람과 모르는 사람 간에는 그 대응에서 확연한 차이가 날 것