[잡동사니] 테스트 - 잘나오나여

		제 3장
조화가진 진동
	기계시스템이나 구조시스템이 진동하는 동안 외부 에너지가 계에 공급되면 그 계는 강제진동을 한다고 말한다. 외부 에너지는 가해진 힘이나 변위 가진을 통해 계에 공급될수 잇다. 가해진 힘이나 변위 가진은 조화적·비조화적이거나 주기적·비주기적 또는 불규칙적일수 있다. 조화가진에 대한 계의 응답을 조화응답이라고 한다. 비주기적인 가진은 길거나 짧은 지속시간을 가질 수 있다. 갑자기 작용한 비주기적 가진에 대한 동역학계의 응답을 과도응답이라 한다. 이 장에서는 조화가진을 받는 1자유도계의 동적 응답을 고찰해보기로 하자. 조화가진은 또는 또는 의 형태이며 ,는 각각 조화가진의 진폭, 진동수, 위상각이다. 의 값은 에서 일때의 값에 달려 있으며 보통 0으로 취한다. 조화가진을 받는 계의 응답은 역시 조화적이다. 만약 가진의 진동수와 고유 진동수가 일치할 경우 그 계의 응답은 매우 커지게 된다. 공진이라 부르는 이러한 조건은 계의 파손을 방지하기 위해 피해야 한다. 불평형 회전 기계에서 발생하는 진동, 정상상태의 바람 속에서 와류유출로 인한 높은 굴뚝의 진동, 사인파형의 노면 위에서 자동차의 연직 운동은 조화적으로 가진된 진동의 예들이다.

3.1

운동방정식

가진을 받는 m-c-k 시스템의 경우 다음과 같은 운동방정식을 세울 수 있다.

여기서 가진의 경우 위에서 언급한 3가지의 종류를 살펴보겠다.

3.2

비감쇠계의 응답

비감쇠걔(c=0)의 경우로서 다음과 같은 운동방정식을 가진다.

이 방정식의 재차해는 다음과 같다.

이때 은 고유진동수이다.

가진력 가 조화적이므로 특별해 역시 조화적이고 같은 진동수w를 같는다. 따라서 다음과 같은 형태의 해를 가정한다.

여기서 X는 의 최대진폭을 나타내는 상수다. 여기서 X에 대해 풀면 다음과 같은 식이 나온다.

이때 는 힘 를 받는 질량의 처짐을 나타내고, 가 일정한 힘이므로 정적 변형이라 한다. 따라서 이 식의 전체해는 다음과 같다.

초기조건 와 를 사용하면 다음을 얻는다.

이를 대입하여 정리하면 다음과 같은 전체해가 나온다.

여기서 가진의 진폭에 대해서 고찰해 보자

가진의 진폭 X를 다음과 같이 표기할수 있다.

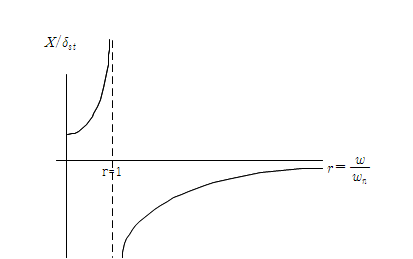
이때 는 운동의 동적 진폭의 정적 진폭에 대한 비를 나타내며 확대율,증폭율,진폭비라 한다. 진폭비 의 진동수비 에 대한 변화를 다음과 같이 도식화 할 수 있다.

3.2.1 맥놀이 현상

 가진진동수와 계의 고유진동수와 정확히 같지는 않고 이에 가까우면 맥놀이라는 현상이 일어난다. 이러한 형태의 진동에는 진폭이 규칙적으로 증가하고 다시 감소한다. 맥놀이 현상은 다음의 식을 보면서 간단히 고찰할수 있다.

초기조건이 0으로 취하면 위의 해는 간단히 쓸수 있게 된다.

,이다.

이며, 이를 대입하면

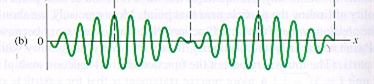
여기서 은 작은 값이기 때문에 함수 는 적게 변하고 주기 은 크다. 따라서 이 함수는 변화하는 진폭 을 갖는 진동을 가진다.

위 그림에서 보듯이 wt곡선이 한 사이클을 이루는 동안 는 여러 사이클을 완성하는 것을 볼 수 있다. 이처럼 진폭은 끊임없이 증가하고 감소한다. 진폭이 0인 점 사이 또는 진폭이 최대인 점 사이의 시간을 맥놀이 주기라 부르고

로 주어지며 맥놀이 주파수는 다음과 같이 정의된다.

댓글 : 2 개

• ★이동국★
• 2012/05/10 PM 07:12

뭐라는데 지금

• 메르꾸리오
• 2012/05/10 PM 09:23

제 정신을 테스트 당한거 같아요.....

친구글 비밀글 댓글 쓰기

[★이동국★]

뭐라는데 지금

[메르꾸리오]

제 정신을 테스트 당한거 같아요.....