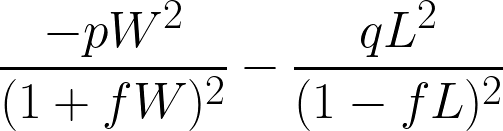도입
배팅을 할 때 내가 가진 돈의 몇 퍼센트를 배팅해야 나의 수익이 극대화될까. 승률이 100%라면 고민할 필요 없이 내가 가진 돈의 전부를 배팅하면 그만이다. 하지만 승률이 100%가 아니라면?
40%의 확률로 도박사가 배팅한 돈을 3배로 돌려주고, 60% 확률로 도박사가 배팅한 돈 전부를 가져가버리는 어떤 도박장을 가정해보자. 100원을 배팅할 경우 기대 수익은
200원 × 0.6 - 100원 × 0.4 = 80원
이므로 굉장한 이득을 가져다주는 배팅이다. 따라서 가진 돈의 전부를 배팅하는 것이 수익을 극대화할 수 있는 것일까?
가진 돈의 전부를 건 사람은 언젠가 반드시 빈털터리가 된다는 것이 이 도박장의 함정이다. 100만 원의 판돈을 가지고 항상 전부를 배팅하는 도박사가 정말 운이 좋게 10판 연속으로 승리했다고 가정해보자. 덕분에 100만 원으로 시작한 돈이 590억이 넘는 큰돈이 되었다. 그리고 이 돈을 다시 11판째에 배팅하여 이번엔 패배하였다(승률이 40%인 게임에서 10번 연속으로 이기고 1번 진 것이라면 충분히 지나치게 운이 좋은 사람이다). 그 전까지의 행운에도 불구하고 그가 가진 돈은 0원이 되었다. 한판이라도 지면 전부를 잃게 되는 게임이기 때문이다.
하면 할수록 유리한 게임인 거 같은데, 몰빵을 하면 언젠가는 빈털터리가 되고 만다. 그렇다면 대체 내가 가진 돈의 몇 퍼센트를 투자해야 이 도박판에서 최고의 수익을 낼 수 있을까?
켈리에 따르면 저 도박판에서 도박사는 매번 배팅마다 가진 돈의 10%만을 배팅해야 한다.
증명
여기서는 고등학교 수학 수준에서 간단한 증명을 해보자.
1)
도박에서 승리할 확률을 p, 도박에서 패배할 확률을 q = 1 - p, 도박에서 승리했을 때 수익률을 W, 도박에서 패배했을 때 손실률을 L, 총 배팅 횟수를 N, 승리한 횟수를 Nw, 패배한 횟수를 Nl이라 하자. 그리고 매번 배팅하는 비율을 f라 하자.
p: 승리할 확률
q: 패배할 확률
W: 승리시 수익률
L: 패배 시 손실률
f: 배팅 비율
N: 총 배팅 횟수
Nw: 총 배팅 중 승리한 횟수
Nl: 총 배팅 중 패배한 횟수
2)
소유 금액에서 f 비율만큼 배팅하여 승리하면 소유 금액은 (1 + f*W) 배가 된다. 반면, 소유 금액에서 f 비율만큼 배팅하여 패배하면 소유 금액은 (1 - f * L) 배가 된다.
따라서 만약 총 N번의 배팅을 하는 동안 Nw번 이기고, Nl번 졌다면 소지 금액은

배가 된다(식1).
수익률을 극대화시키려면 위의 배율이 최대화되어야 한다.
3)
N번의 배팅으로 위의 배율이 된다면, 1번의 배팅으로는 위의 수치의 기하평균만큼의 배율이 될 것이다. 즉 전체에 (1/N) 승을 하여

배가 된다(식 2).
이때 N이 충분히 크다면 이 값은

위의 값으로 대신할 수 있다(식 3).
4)
식 3에 자연로그를 씌우면

이 된다(식 4).
당연히 이 식 4가 최대화될 때 식 3도, 식 2도 식 1도 최대화된다.
5)
식 4가 최대화되는 f를 찾기 위해 식 4를 f로 미분한다. 그러면

이 된다(식 5). 이 식 5가 0이 되는 점에서의 f는

이 된다(식 6).
즉, f가 식 6을 만족할 때 식 4는 극대 혹은 극소가 된다.
6)
식 6의 f가 극대점인지 극소점인지 확인하기 위해 식 5를 다시 미분하여 식 4의 f에 대한 이계도함수를 구하면
이 된다(식 7). 식 7은 항상 0보다 작다. 따라서 식 6을 만족하는 f는 식 4를 최대로 만드는 점이다.
결론)
배팅을 할 때 수익을 극대화시켜주는 배팅 비율인 캘리 비율 f는 아래와 같다.

p: 승리 확률
q: 패배 확률
W: 승리했을 때 수익률
L: 패배했을 때 손실률
쓰다 보니 길어졌지만 그냥 수익의 기하평균값을 극대화시켜주는 비율을 찾으면 되는 간단한 계산이다.
마무리
이제 도입 부분에서 예시로 들었던 도박장에서 수익을 최대화시켜주는 배팅 비율을 켈리 비율을 통해 구해보자.
승률이 40% 이므로 p = 0.4, q = 0.6이다.
승리했을 때 배팅한 돈을 3배로 돌려주므로 수익률은 200%니까 W = 2, 패배했을 때 배팅한 돈 전부를 잃게 되므로 손실률은 100%니까 L = 1이다. 따라서, 도박사의 수익을 극대화하는 배팅 비율 f는

10%이다.
도박사는 매번 배팅마다 자신이 보유한 금액의 10%를 배팅해야 한다.
참고로 f가 0보다 작은 값이 나온다면 배팅하지 말아야 할 도박이라는 뜻이다.
+)
이번엔 다른 도박장을 생각해보자. 이 도박장은 한번 배팅을 하면 1년 후에 결과가 나온다. 그리고 어떤 도박사 A는 이 도박장에 배팅하려고 이 도박장을 연구 중이다.
A가 그 도박장을 연구해보니 일반적인 도박사들은 10년에 9년은 승리하고 1년은 패배한다. 그리고 본인도 아마 승률이 비슷할 것이라고 생각된다. 따라서 승리할 확률 p = 0.9, 패배할 확률 q = 0.1이라고 추정하였다.
그리고 도박사들은 일반적으로 승리하였을 때는 11%의 수익을 얻고, 실패하였을 때는 50%의 손실을 입었다. 따라서 승리하였을 때 수익률 W = 0.11, 실패하였을 때 손실률 L = 0.5라고 추정하였다.
A는 매년 본인이 자신 돈의 몇 퍼센트를 배팅해야 할지 정하기 위하여 켈리 비율을 사용하기로 마음을 먹었다. 켈리 비율에 따르면, 최적의 배팅 비율 f는
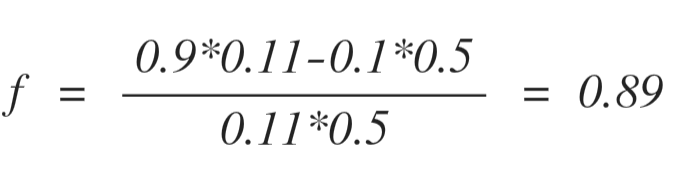
0.89, 즉 89%다.
투자할 때 켈리 비율을 참고한다는 버핏이 항상 현금 비중을 일정하게 유지하는 이유를 이해할 수 있다.