산타랠리는철지난 미신일 뿐
정량적이고 합리적 분석이 주를 이룰 것 같은 금융시장에는 의외로(?) 미신(superstition)이 많이 존재하는데, 산타랠리도 그 중 하나로 볼 수 있다. 산타랠리는 1972 년 예일 허시라는 이코노미스트가 처음 사용한 용어로, 정확하게는 마지막 5 거래일과 새해 첫 2 거래일 동안 주식시장이 상승하는 계절적 패턴, 즉 계절성을 일컫는다. 시장은 통상적으로 월간 기준으로 12월을 산타랠리로 지칭하기도 하며, 유사한 캘린더 효과로 1월 효과 또한 존재한다.
주가도 엄연히 금융 시계열(time-series)이기 때문에 계절성은 당연히 존재할 수 있다. 다만 단순히 과거 상승했던 달의 비율, 또는 평균 수익률 등이 상대적으로 높다고 해당 계절성이 통계적으로 유의하다고 주장하는 것은 지나치게 나이브한 접근이며, 자칫 개인투자자와 같은 비전문가를 오도할 수 있다. 비단 산타랠리뿐만 아니라 시계열 자체의 기술적 분석, 그리고 적절한 마켓 타이밍 선정을 위해 계절성을 검증한다면 반드시 통계적 유의성을 검증할 필요가 있다.
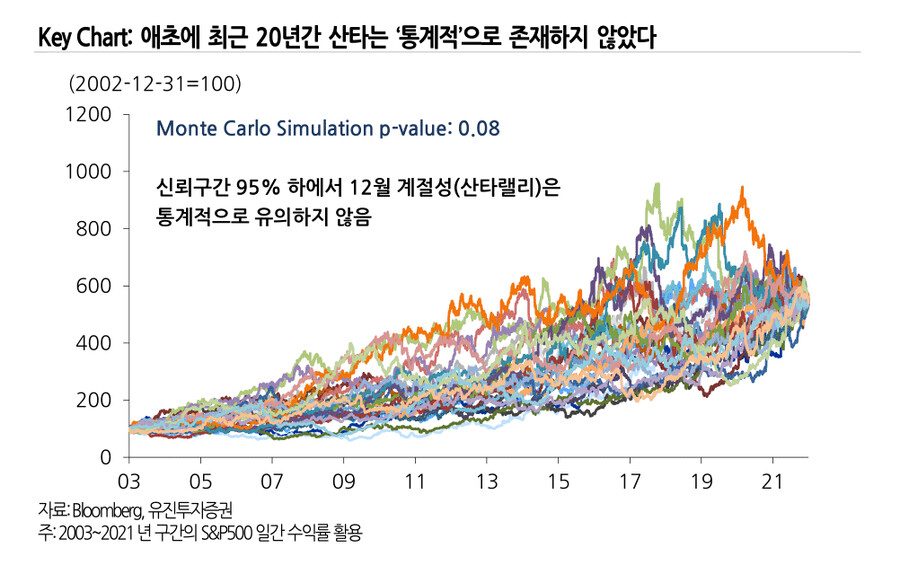
이번 자료에서는 시계열의 계절성 검증을 위한 간단한 방법론을 소개하고자 한다. 통계학에서 말하는 p-value는 특정 사건(관찰된 값)이 우연히 발생할 확률이라고 해석할 수 있다. 통상적으로 p-value 가 0.05 보다 작으면 해당 사건이 통계적으로 유의하다고 볼 수 있는데, 이는 이 사건이 우연히 일어났을 가능성이 매우 낮다고 추정하는 것이다. 간단한 몬테카를로 시뮬레이션을 활용하면 계절성의 p-value를 추정해볼 수 있다. S&P500 의 경우 최근 20 년간 12 월, 그리고 연 마지막 주간의 상승 비율에 대한 p-value 는 각각 0.09, 0.67 로, 0.05 보다 높다. 산타랠리는 통계적으로 유의한 계절성이 아닌 것으로 판단할 수 있다.
계절성을 통계적으로 검증하는 법
: 특정 사건이 우연하게 발생했을 가능성: p-value
통계학에서 p-value 의 정의는 다음과 같다.
"귀무가설이 맞다고 가정할 때, 관찰된(또는 그보다 더 극단적인) 결과가 나타날 확률"
귀무가설(Null Hypothesis)과 같은 새로운 용어 때문에 어려워보일 수 있으나 p-value 의 개념은 단순하다. 현실에서의 모든 금융 시계열에 대해 우리가 관측 가능한 시계열은 단 하나다. 하지만 우리는 금융 시계열이 특정 부분 랜덤하게 움직인다는 사실을 알고 있다. 즉, 우리가 관측한 시계열에서 나타난 특정 현상(계절성 등)이 실제로는 랜덤한 움직임으로 인해 우연히 발생했을 가능성 또한 존재한다는 것이다. p-value 는 그 가능성을 측정하는 척도로, 특정 현상이 우연하게 발생할 확률로도 해석할 수 있다. 통상적으로 p-value 가 0.05 보다 작으면 해당 현상이 통계적으로 유의하다고 해석한다.
귀무가설이 맞다고 가정하는 이유를 이해하기 위해서는 중심극한정리 등의 개념에 대한 이해가 선행돼야 하지만 이에 대한 설명은 생략하겠다. 일반적으로 우리가 증명하고자 하는 가설에 반대되는 가설을 귀무 가설로 설정한다. 산타랠리의 계절성을 적용하여 p-value 의 정의를 다시 내려보자.
"실제 시계열에서 나타난 계절성(산타랠리)이 존재하지 않는다고 가정할 때, 실제 시계열만큼의 계절성이 나타날 확률"
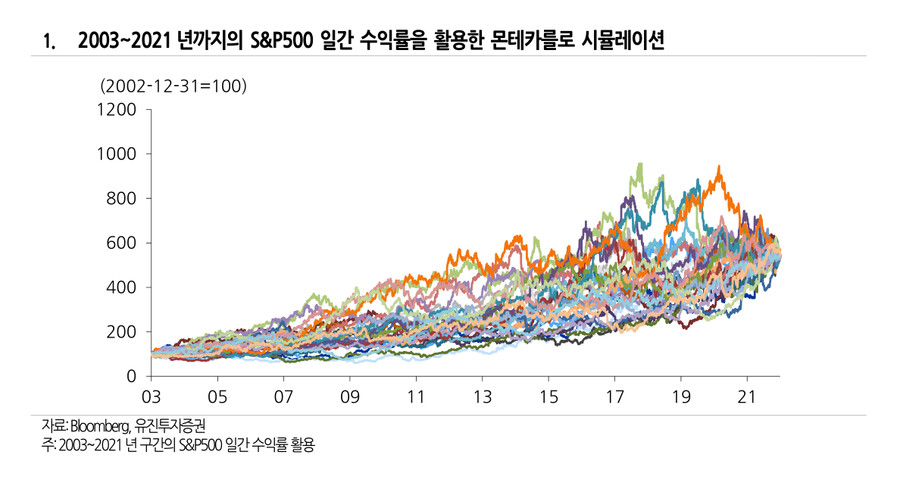
여기서 주의할 점은 귀무가설을 “계절성이 존재하지 않는다”가 아닌 “실제 시계열에서 나타난 계절성이 존재하지 않는다”고 설정한 것이다. 우리는 주식 수익률에 대한 몬테카를로 시뮬레이션을 통해 실제 시계열과 평균과 분산이 동일하지만 다른 움직임을 나타내는 수많은 ‘우연한’ 경우를 생성할 것이다. 수많은 우연한 경우에서는 실제 시계열에서 나타난 계절성이 나타나지 않게 되고(정확히는 그럴 가능성이 높다), 이는 귀무가설을 만족시킨다. 수많은 우연한 경우의 수를 만듦으로써 우리는 대략적으로 p-value 를 추정할 근간을 마련할 수 있다. 도표 1 번은 03~21 년 구간의 S&P500 일간 수익률을 활용한 몬테카를로 시뮬레이션 결과를 보여준다. 실제로는 10,000 회 진행하였다.
산타가 찾아왔다는 착각
: 산타랠리 계절성은 통계적으로 유의하지 않아
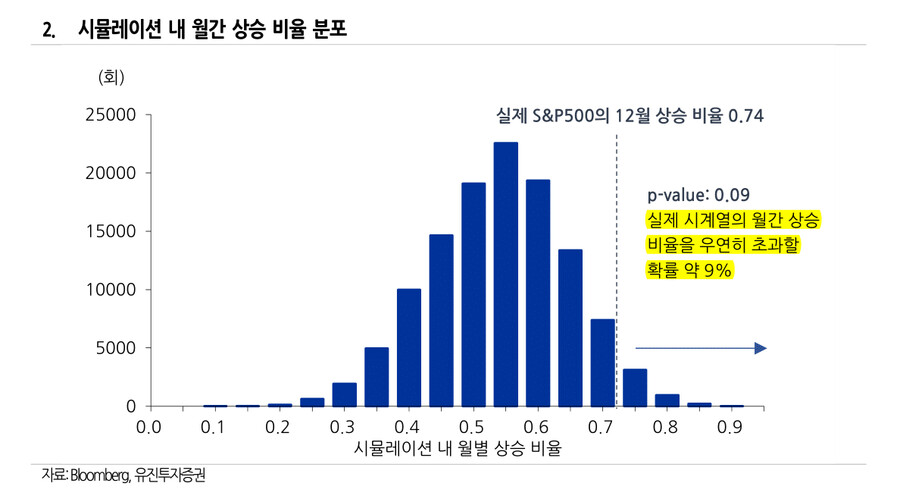
몬테카를로 시뮬레이션을 통해 수많은 우연한 경우의 수(분모)가 마련됐으니, 이제 분자가 필요하다. 즉, 수많은 우연한 경우의 수가 준비됐으니 실제 시계열 수준 이상의 계절성이 나타나는 경우의 수를 구해야 한다. 이때 실제 시계열의 계절성 정도는 전체 구간(03~21 년)에서 12 월에 월간으로 상승한 비율로 설정한다. S&P500 기준 12 월에 상승한 비율은 0.74 다. 4월의 0.84 보다 낮고 5,7,11 월과 동일한 수준이다. 이 상승비율만 따져봐도 산타랠리의 계절성이 통계적으로 유의하지 않을 것이라고 어느 정도 유추 가능하다.
12월 계절성 수준을 활용하여 실제 p-value를 계산해보면 0.09가 나온다. 이는 우연히 월간으로 12월보다 같거나 더 높은 계절성이 나타날 확률이 9%라고 해석할 수 있다(도표 2 번). 기존 산타랠리의 정의에 맞게 각 연도의 마지막 주간을 기준으로도 p-value 는 0.67 수준으로 오히려 높아진다. 즉,최근 20년 기준으로는 산타랠리는 통계적으로 어떤 의미도 가지지 않는다. 어쩌면 우리는 부모님(무작위성)이 두고 간 선물을 보며 매년 산타가 찾아왔다는 착각을 했을 수 있다. 오히려 산타랠리를 검증하는 과정에서 의외의 계절성 효과를 발견했다. 4월 기준의 계절성 검증에서 p-value는 0.0087로 0.01보다도 낮은 수준으로 나타난다. 즉, 4월 효과는 신뢰구간 99%에서 통계적으로 유의하다고 볼 수 있다. 하지만 계절성 그 자체를 마켓 타이밍 관점에서 적극적으로 활용하는 것은 지양할 필요가 있다. 지난 4월 월간으로 S&P500 은 -8.8% 하락했다. 시간만을 변수로 하여 움직이는 계절성은 무조건적으로 신뢰할 수 있는 기술적 지표가 아니다.
- 유진투자증권 크로스에셋/AI 전략 허석민 -