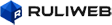직각 삼각형의 빗변의 제곱은 다른 두 변의 제곱의 합과 같다.
이 정리는 매우 중요하며, 여러 곳에서 응용되고 있다. 이 정리는 BC 500년경, 그리스인 피타고라스가 발견하였다고 되어 있으나 특별한 경우는, 그보다 훨씬 이전에 알려져 있었다고, 독일의 유명한 역사학자 칸토르는 말하고 있다.
<파피루스>를 보면, 이집트 사람은 BC 2300년경, 3 : 4 : 5 의 길이를 이용하여 직각을 만들었으며, 인도에서는 BC 400∼500 년경 15, 36, 39를 세 변으로 하는 삼각형으로 이미 직각을 만들었다고 한다. 중국에서는 3000년에 진자에 의해 발견되었다고 해서 진자의 정리로 부르기도 한다.
32 + 42 = 52 , 152 + 362 = 392
그러나 피타고라스에 이르러 비로소 이 정리가 일반적으로 알려졌다고 한다. 우리들이 공부하는 기하학은 탈레스에 의해 최초로 조직화되었고, 피타고라스에 의해 일반인에게 교육되었다.
이 유명한 정리의 증명법은 피타고라스 이후 많은 학자들이 연구하여, 가능한 모든 방법이 전부 찾아진 것으로 생각되며 그 방법의 총 수는 280가지 그 이상이라고 한다.
피타고라스의 정리를 증명하는 방법은 닯은 직각삼각형의 변의 길이 사이의 비례관계를 이용하는 것과 같은 대수적인 증명법, 넓이의 비교를 통한 기하학적 증명법, 벡터를 이용한 증명법, 힘의 개념을 이용하는 동역학적인 증명법 등 대단히 많다. 또 이 정리는 일반 삼각형에서의 제2코사인법칙의 특별한 경우로 볼 수 있다.
증명을 하면서 수학이 아름답다는 것을 다시 한번 깨닫는다. 하나의 문제를 이렇게 다양한 각도에서 바라보고 생각할 수 있다는 것이 그저 놀랍고 신기할 따름이다. 플레시나 자바를 이용하여 한 눈에 알아볼 수 있는 수학보다 좀 힘들지만 생각해서 알아내는 수학이 더 재미있다. 증명을 이리 굴리고 저리 굴리면서 어렵사리 이해해냈을 때의 그 감동을 어찌 말로 할 수 있을까! 생각해보자. 그리고 행복한 미소를 지어보자. 이렇게 많은 증명 중 몇 가지를 보기로 들어본다.