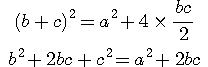미국 대통령 중 몇 명은 수학과 미약한 관계를 유지했었다.
워싱턴(George Washington)은 유명한 측량가였고,
제퍼슨(Thomas Jefferson)은 미국에서 고등 수학을 가르칠 것을 장여하려고 많은 노력을 했으며,
링컨(Abraham Lincoln)은 유클리드의 '원론'을 공부함으로써 논리를 배웠다는 이야기가 있다.

더욱 독창적이었던 사람은 20대 대통령 가필드 (James Abram Garfield, 1831-1881)였는데,
그는 학창 시절에 초등수학에 대한 강렬한 흥미와 상당한 재능을 갖고 있었다.
그가 독창적으로 피타고라스 정리에 대한 멋진 증명을 발견했던 시기는.
그가 대통령이 되기 5년 전인 하원의원 시절이었던 1876년이었다.
그는 다른 상원의원들과 수학에 대해서 토론을 하던 중에 그 증명이 떠올랐는데,
그 증명은 뒤에 뉴잉글랜드 교육잡지에 게재되었다.
이 증명은 사다리꼴의 넓이에 대한 공식을 배운 즉시 제시될 수 있다.

(참고 : 수학의 위대한 순간들, 경문사, H.Eves, pp39-41)

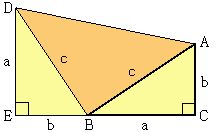
1876년 가필드가 발표한 교묘한 증명 방법

□ DECA = △ DEB + △ ABC + △ DBA

∴ a2 + b2 = c2

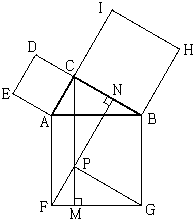
C, F에서 AB, BC에 수선 CM, FN을 내려 그 교점을 P라고 하면

FN ⊥ PG
∴ △ ABC ≡ △ CPN ≡ △ PFG

∴ □ CAFP = AC · CN = AC2
같은 방법으로
□ CPGB = BC2


*누구의 증명인지 모를 경우에는 증명법에 따라 번호를 붙이고 있다.

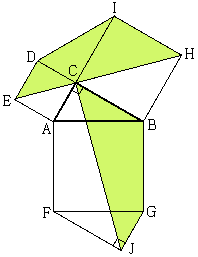
이 그림은 레오나르도 다 빈치(Leonardo da Vinci, 1452-1519)가 고안했던 것이라고 한다.

그림에서

AC // JG, BC // FJ 되게 하면
△ ABC ≡ △ CID ≡ △ FJG
□ IDEH ≡ □ EABH ≡ □ CAFJ ≡ □ JGBC
∴ ABHIDE = CAFJGB
∴ ABHIDE - 2△ABC = CAFJGB - 2△ABC
∴ □ ACDE + □ CBHI = □ AFGB

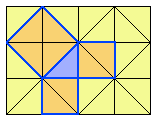
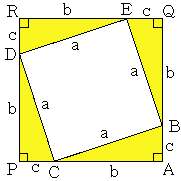
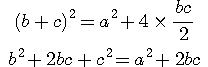
피타고라스는 당시 사원의 보도 블록을 보고 이 정리의 힌트를 얻었다고 한다.
그림을 보자. 하늘색 직각삼각형의 주위를 유심히 보면, 빗변 위에 그려진 정사각형에는 보도 블록 4개가 들어가고
다른 변 위에 그려진 정사각형에는 각각 2개씩 들어간다.
2+2=4 는 너무도 자명하다. 이것은 직각이등변 삼각형의 경우이지만 피타고라스는 이것을 더욱 일반화하여 일반적인 직각삼각형의 경우에까지 적용했으리라는 추측이다.

데오게네스 라에주스와 플루타크는 "이 정리를 발견한 피타고라스는 너무 기뻐서 그 공을 신에게 돌리며 황소 100마리를 잡아 감사의 제물로 바쳤다"라고 전하고 있다. 그러나 이 이야기에 대해서는 여러 가지 반대설도 있으며, 피타고라스는 "영혼은 불멸하고 윤회 이전하는 것"이라고 믿었으므로 피를 흘리는 것을 좋아하지 않았기 때문에 신에게 바친 것도 살아있는 소가 아니고, 밀가루로 만든 소 한 마리였다고 주장하고 있다.

직각 삼각형의 빗변의 제곱은 다른 두 변의 제곱의 합과 같다.

이 정리는 매우 중요하며, 여러 곳에서 응용되고 있다. 이 정리는 BC 500년경, 그리스인 피타고라스가 발견하였다고 되어 있으나 특별한 경우는, 그보다 훨씬 이전에 알려져 있었다고, 독일의 유명한 역사학자 칸토르는 말하고 있다.

<파피루스>를 보면, 이집트 사람은 BC 2300년경, 3 : 4 : 5 의 길이를 이용하여 직각을 만들었으며, 인도에서는 BC 400∼500 년경 15, 36, 39를 세 변으로 하는 삼각형으로 이미 직각을 만들었다고 한다. 중국에서는 3000년에 진자에 의해 발견되었다고 해서 진자의 정리로 부르기도 한다.

32 + 42 = 52 , 152 + 362 = 392

그러나 피타고라스에 이르러 비로소 이 정리가 일반적으로 알려졌다고 한다. 우리들이 공부하는 기하학은 탈레스에 의해 최초로 조직화되었고, 피타고라스에 의해 일반인에게 교육되었다.

이 유명한 정리의 증명법은 피타고라스 이후 많은 학자들이 연구하여, 가능한 모든 방법이 전부 찾아진 것으로 생각되며 그 방법의 총 수는 280가지 그 이상이라고 한다.

피타고라스의 정리를 증명하는 방법은 닯은 직각삼각형의 변의 길이 사이의 비례관계를 이용하는 것과 같은 대수적인 증명법, 넓이의 비교를 통한 기하학적 증명법, 벡터를 이용한 증명법, 힘의 개념을 이용하는 동역학적인 증명법 등 대단히 많다. 또 이 정리는 일반 삼각형에서의 제2코사인법칙의 특별한 경우로 볼 수 있다.

증명을 하면서 수학이 아름답다는 것을 다시 한번 깨닫는다. 하나의 문제를 이렇게 다양한 각도에서 바라보고 생각할 수 있다는 것이 그저 놀랍고 신기할 따름이다. 플레시나 자바를 이용하여 한 눈에 알아볼 수 있는 수학보다 좀 힘들지만 생각해서 알아내는 수학이 더 재미있다. 증명을 이리 굴리고 저리 굴리면서 어렵사리 이해해냈을 때의 그 감동을 어찌 말로 할 수 있을까! 생각해보자. 그리고 행복한 미소를 지어보자. 이렇게 많은 증명 중 몇 가지를 보기로 들어본다.